안전지대

나에게는 상당히 어려운 문제였다.
지뢰가 있는 칸과 그 주변 8칸이 위험지역이고, 안전지역의 수를 계산해서 return해야 하는 문제다. 처음에는 지뢰의 위치에 따라 주변의 위험지역을 계산해 보려 했는데 고려해야 할 경우의 수가 너무 많아 잘 안 됐다. 그래서 고민하던 중, for 반복문을 이용해 모든 칸을 돌면서 위험지역인지 여부만 판단하는 방식으로 바꾸어서 푸니 보다 쉬워졌다.
class Solution {
public int solution(int[][] board) {
int answer = n * n;
for (int i = 1; i < board.length; i += 3) {
for (int j = 1; j < board[i].length; j += 3) {
if (board[i][j] == 1) {
answer -= 9; // 위험지역 9칸
if (board[i + 1][j] == 1 && board[i + 2][j] != 1) {
answer -= 3; // 위험지역 3칸 추가
} else if (board[i + 2][j] == 1) {
answer -= 6; // 위험지역 6칸 추가
}
if (board[i - 1][j] == 1) {
answer += 6; // 위험지역 6칸 취소
} else if (board[i - 2][j] == 1 && board[i - 1][j] != 1]) {
answer += 3; // 위험지역 3칸 취소
}
if (board[i][j + 1] == 1 && board[i][j + 2] != 1) {
answer -= 3; // 위험지역 3칸 추가
} else if (board[i][j + 2] == 1) {
answer -= 6; // 위험지역 6칸 추가
}
if (board[i][j - 1] == 1) {
answer += 6; // 위험지역 6칸 취소
} else if (board[i][j - 2] == 1 && board[i][j - 1] != 1) {
answer += 3; // 위험지역 3칸 취소
}
if (board[i + 1][j + 1] == 1) {
}
}
}
}
// 0,0 0,n n,0 n,n 4칸
// 0,i n,i i,0 i,n 6칸
// 나머지 9칸
return answer;
}
}
처음에 짜던 조잡한 코드다. 지뢰 매설 지역을 기준으로 주변 9칸을 계산하며 위험지역을 계산하는 방식이다. 중복을 피하기 위해 i는 3씩 증가하면서, 하나의 i당 주변 24칸의 지뢰 존재 여부에 따라 추가해야 할 위험지역의 넓이가 변한다. 경우의 수가 너무 많아 짜던 중 포기하고 아래의 방식으로 바꾸게 되었다.

역시 길고 조잡한 코드다. 하지만 설계하기는 비교적 쉬웠다. 모든 지역을 돌면서 해당 지역이 위험한지 아닌지 판단하고, 위험지역일 때마다 answer의 초기값인 n * n 에서 1씩 빼 주는 방식이다. 반대로 answer의 초기값을 0으로 시작해 안전지역의 수만큼 더해 주는 방식도 상관없다. 이 때는 조건식의 ||를 &&로 바꿔 주면 된다. 해당 위치와 주변 3칸, 즉 4칸의 지뢰 존재 여부에 영향을 받는 꼭지점 부분과, 6칸의 영향을 받는 변 부분, 9칸의 영향을 받는 내부 부분으로 나눠 계산했다.
어김없이 에러가 발생했는데, 60개나 발생해 버렸다. 이로써 기쁘게도 에러 수 최고 기록을 경신하게 되었다.

가장 먼저 눈에 띄는 에러는 놀랍게도 answer의 초기값인 n * n의 변수 n이 선언되지 않아서 발생한 문제였다. 제한사항에서 board가 n * n 배열이라는 설명을 읽고 나도 모르게 n이 이미 존재하는 걸로 착각했다.

n을 선언해 주니 굉장히 많은 에러가 사라졌음에도, 아직 27개나 남아 있다.

다음으로 해결한 문제는 6칸짜리 for문에서 i를 선언하지 않고 i = 1 로 초기화를 한 것이다. 9칸짜리에는 또 선언이 되어 있는데, 식이 복잡하다 보니 나도 정신이 없는 모양이다.
다른 문제는 위에 나와 있듯이 ArrayIndexOutOfBoundsException이 발생한 것이다. 배열의 index가 범위를 넘어갔다는 것이다. i - 1의 범위 초과는 고려해서 i를 1부터 시작해 놓고, 위쪽 i + 1의 범위 초과는 고려를 안 하고 그냥 n보다 작은 i까지로 넣었다. 이렇게 하면 배열 board의 길이보다 큰 index를 계산하게 되어 버린다. 따라서 범위 제한을 n - 1 로 줄여 줘야 한다.

테스트를 통과하고 성공한 줄 알았으나, 정확성이 88.9%로 나온다. 논리는 분명 틀리지 않았다. 경우의 수도 빠짐없이 고려했다. 런타임 에러가 왜 발생했는지도 알 수 없었다.

원인은 board가 1칸짜리인 경우를 고려 못 한 것이다. 정말 허무한 원인이다. 경우의 수를 따질 때에는 가장 단순한 case부터 분류해 나가야 모든 case가 빠짐없이 고려될 것이다. 나는 크고 복잡한 case를 푸는 방법에 매몰돼 이런 실수를 해 버린 것이다. 최상단에 1칸짜리인 case를 추가하니 드디어 통과할 수 있었다.

엄청 길어서 정성추로 좋아요를 많이 받고 올라간 풀이다. 1줄에 짧게 쓸 수 있는 삼항 연산자를 사용하면서도 100줄이 넘어가는 코드를 읽으면서 경의를 표할 수밖에 없었다. 300줄이 넘어가는 훨씬 긴 풀이도 있는데, 같이 올리면 글이 너무 길어질 것 같다.

board 배열의 길이를 늘려 꼭지점과 변의 경우의 수를 따로 나누지 않고 쉽게 계산할 수 있게 했다. 전혀 생각을 못 했다. 하지만 지금 배웠으니 다음에 비슷한 문제가 나오면 분명 활용할 수 있을 것이다.
겹치는 선분의 길이

처음 문제를 접했을 때는 어렵지 않아 보였는데, 역시 정답률이 낮은 데는 이유가 있었다. 앞의 문제보다도 푸는 데 훨씬 더 오래 걸렸던 문제다. 내가 생각해도 정말 엄청난 시간을 갈아 넣었다.
위의 다른 풀이에 나도 모르게 영향을 받았는지, 내가 처음에 시도했던 코드는 모든 경우의 수를 일일이 계산하는 방식이었다. 너무 길어서 화면에 전부 담기지 않아, 직접 복사해서 올려야 할 정도다.
class Solution {
public int solution(int[][] lines) {
int answer = 0;
// 두 선분만 겹칠 때
// index[0][0] 이 lines[1][0] 보다 작거나 같은 경우
if (lines[0][0] <= lines[1][0] && lines[1][0] <= lines[0][1]) {
if (lines[0][1] <= lines[1][1]) {
answer += lines[0][1] - lines[1][0];
} else {
answer += lines[1][1] - lines[1][0];
}
}
// index[1][0] 이 lines[0][0] 보다 작은 경우
if (lines[1][0] < lines[0][0] && lines[0][0] <= lines[1][1]) {
if (lines[1][1] <= lines[0][1]) {
answer += lines[1][1] - lines[0][0];
} else {
answer += lines[0][1] - lines[0][0];
}
}
// index[0][0] 이 lines[2][0] 보다 작거나 같은 경우
if (lines[0][0] <= lines[2][0] && lines[2][0] <= lines[0][1]) {
if (lines[0][1] <= lines[2][1]) {
answer += lines[0][1] - lines[2][0];
} else {
answer += lines[2][1] - lines[2][0];
}
}
// index[2][0] 이 lines[0][0] 보다 작은 경우
if (lines[2][0] < lines[0][0] && lines[0][0] <= lines[2][1]) {
if (lines[2][1] <= lines[0][1]) {
answer += lines[2][1] - lines[0][0];
} else {
answer += lines[0][1] - lines[0][0];
}
}
// index[1][0] 이 lines[2][0] 보다 작거나 같은 경우
if (lines[1][0] <= lines[2][0] && lines[2][0] <= lines[1][1]) {
if (lines[1][1] <= lines[2][1]) {
answer += lines[1][1] - lines[2][0];
} else {
answer += lines[2][1] - lines[2][0];
}
}
// index[2][0] 이 lines[1][0] 보다 작은 경우
if (lines[2][0] < lines[1][0] && lines[1][0] <= lines[2][1]) {
if (lines[2][1] <= lines[1][1]) {
answer += lines[2][1] - lines[1][0];
} else {
answer += lines[1][1] - lines[1][0];
}
}
// 세 선분이 겹칠 때
// lines[0][0]이 가장 작은 경우
if (lines[0][0] <= lines[1][0] && lines[0][0] <= lines[2][0] && lines[1][0] < lines[0][1] && lines[2][0] < lines[0][1]) {
if (lines[1][0] <= lines[2][0]) {
if (lines[0][1] <= lines[1][1]) {
if (lines[0][1] <= lines[2][1]) {
answer -= 2 * (lines[0][1] - lines[2][0]);
} else {
answer -= 2 * (lines[2][1] - lines[2][0]);
}
} else {
if (lines[1][1] <= lines[2][1]) {
answer -= 2 * (lines[1][1] - lines[2][0]);
} else {
answer -= 2 * (lines[2][1] - lines[2][0]);
}
}
} else {
answer -= 2 * (lines[0][1] - lines[1][0]);
}
}
// lines[1][0]이 가장 작은 경우
if (lines[1][0] < lines[0][0] && lines[1][0] <= lines[2][0] && lines[0][0] < lines[1][1] && lines[2][0] < lines[1][1]) {
if (lines[0][0] <= lines[2][0]) {
answer -= 2 * (lines[1][1] - lines[2][0]);
} else {
answer -= 2 * (lines[1][1] - lines[0][0]);
}
}
// lines[2][0]이 가장 작은 경우
if (lines[2][0] < lines[1][0] && lines[2][0] < lines[0][0] && lines[1][0] < lines[2][1] && lines[0][0] < lines[2][1]) {
if (lines[1][0] <= lines[0][0]) {
answer -= 2 * (lines[2][1] - lines[0][0]);
} else {
answer -= 2 * (lines[2][1] - lines[1][0]);
}
}
return answer;
}
위의 다른 풀이 1에 비견될 만큼 압도적인 길이다.
여기서 끝난 것이 아니고 세 선분이 겹치는 case를 더 추가해야 한다. 위의 풀이를 보면 lines[0][0] 부분을 추가하다 그만둔 모습이다. 여기까지 작성하고 돌리면 딱 정확도 70%가 나온다.
그러다 문득 프로그래밍이 존재하는 목적을 떠올리게 되었다. 코드를 이렇게 작성할 거면 한 100번까지는 그냥 선분 3개 나올 때마다 사람이 직접 계산하는 게 낫지 않을까? 컴퓨터의 압도적인 연산력을 이용해 복잡한 연산과정을 최대한 자동화하는 것이 프로그래밍의 핵심이다. 이렇게 모든 경우의 수를 일일이 작성하는 코드는 프로그래밍의 본질에서 벗어났다는 생각이 들었다. 그래서 전부 갈아엎고 처음부터 새로운 코드를 짜게 되었다.
class Solution {
public int solution(int[][] lines) {
int answer = 0;
int a1 = lines[0][0];
int b1 = lines[0][1];
int a2 = lines[1][0];
int b2 = lines[1][1];
int a3 = lines[2][0];
int b3 = lines[2][1];
int resultA1;
int resultA2;
int resultA3;
int resultB1;
int resultB2;
int resultB3;
for (int i = -100; i <= 100; i++) {
if (a1 == i || a2 == i || a3 == i) {
resultA1 = i;
break;
}
}
if (resultA1 == a1) {
a1 = 0;
} else if (resultA1 == a2) {
a2 = 0;
} else {
a3 = 0;
}
for (int i = resultA1; i <= 100; i++) {
if (a1 == i || a2 == i || a3 == i) {
resultA2 = i;
break;
}
}
if (resultA2 == a1) {
a1 = 0;
} else if (resultA2 == a2) {
a2 = 0;
} else {
a3 = 0;
}
for (int i = resultA2; i <= 100; i++) {
if (a1 == i || a2 == i || a3 == i) {
resultA3 = i;
break;
}
}
for (int i = -100; i <= 100; i++) {
if (b1 == i || b2 == i || b3 == i) {
resultB1 = i;
break;
}
}
if (resultB1 == b1) {
b1 = 0;
} else if (resultB1 == b2) {
b2 = 0;
} else {
b3 = 0;
}
for (int i = resultB1; i <= 100; i++) {
if (b1 == i || b2 == i || b3 == i) {
resultB2 = i;
break;
}
}
if (resultB1 == b1) {
b1 = 0;
} else if (resultB1 == b2) {
b2 = 0;
} else {
b3 = 0;
}
for (int i = resultB2; i <= 100; i++) {
if (b1 == i || b2 == i || b3 == i) {
resultB3 = i;
break;
}
}
if (resultA2 < resultB1) {
answer += resultB1 - resultA2;
}
for (int i = resultB1; i < resultB2; i++) {
if (resultA3 <= i) {
++answer;
}
}
return answer;
}
}
방식을 바꿨음에도 코드는 여전히 엄청나게 길다ㅠㅠ
내가 새로이 바꾼 방식은 수의 크기 순서대로 선분의 시작 좌표는 resultA1 ~ resultA3에 넣고, 마지막 좌표는 resultB1 ~ resultB3에 넣는 것이다.
그런데 result들의 초기값을 지정해 주지 않았더니 에러가 발생한다. 코더 입장에서야 for 반복문에 들어갔다 나오면 반드시 값이 생긴다는 걸 알고 있지만 컴퓨터는 그렇지 않을 것이다. 초기값을 지정해 줬다.

테스트 케이스 6개 중 3개는 틀리게 나온다. 테스트 케이스가 6개나 있는 이유는 내가 전의 방법을 사용할 때 누락된 경우의 수를 찾기 위해 계속 추가했기 때문이다.
논리는 완벽해 보이고 누락된 경우의 수도 없어 보인다. 그럼에도 틀리게 나오는 이유를 알 수가 없다.

사실 원인은 어려운 게 아니었는데, 시작점과 끝점들을 result에 대입하는 과정에서 원래 값은 다음 for문에서 다시 등장하지 않도록 0으로 변경했기 때문이다. 이는 각 선분의 시작점이나 끝점이 서로 중복되는 경우를 고려해 다음 for반복문의 시작 카운트를 같은 수로 놓았기 때문에 필요하게 되었다. 하지만 점들의 값의 범위는 -100부터 100까지이므로, 이전 값이 0 이하였다면 0으로 설정한 값이 뒤에도 나오게 된다. 습관적으로 0이면 중복이 안 될 거라 생각한 것이다. 그래서 범위가 중복되지 않는 101로 변경해 주었다.

드디어 통과에 성공했다.
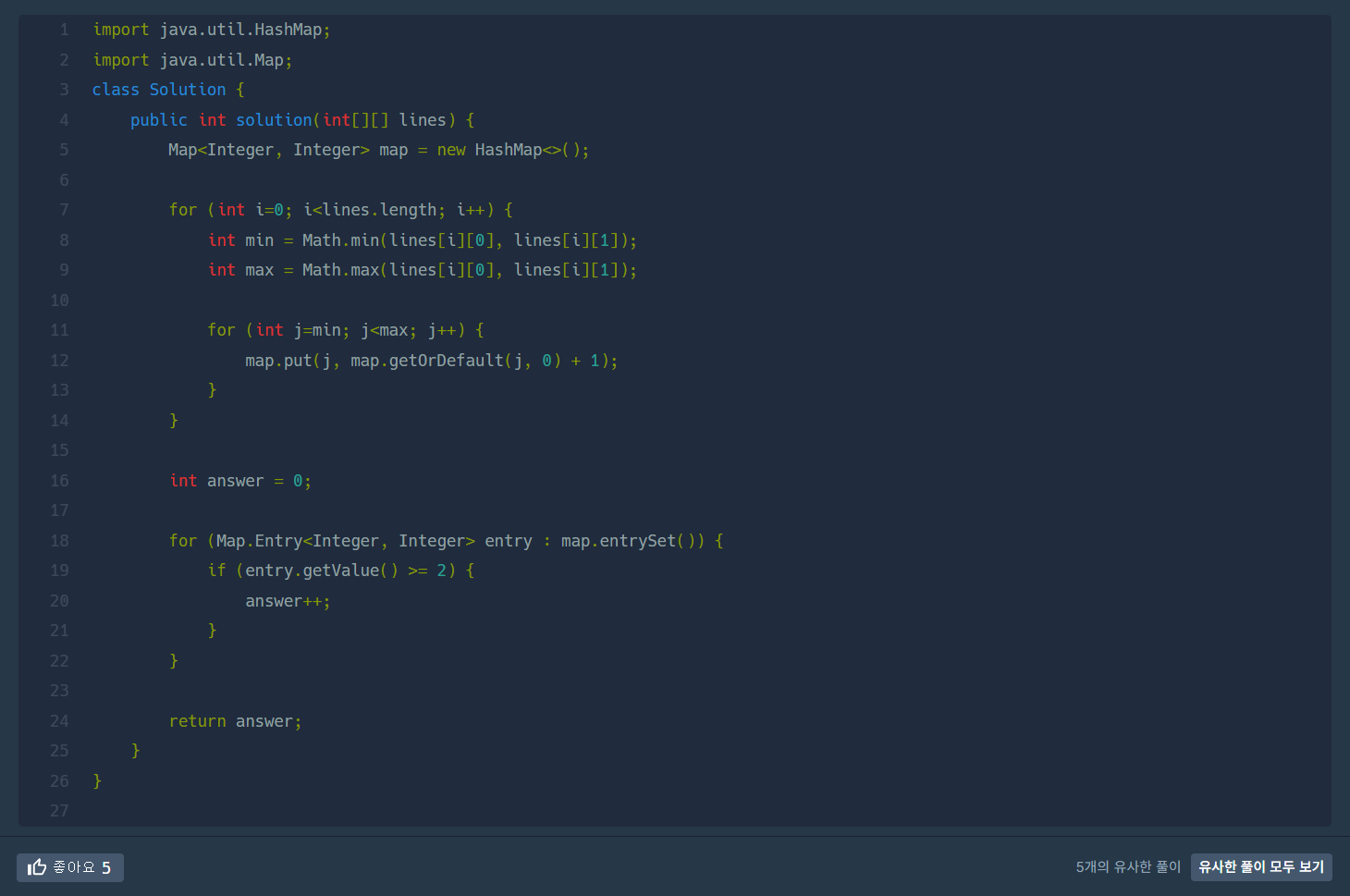

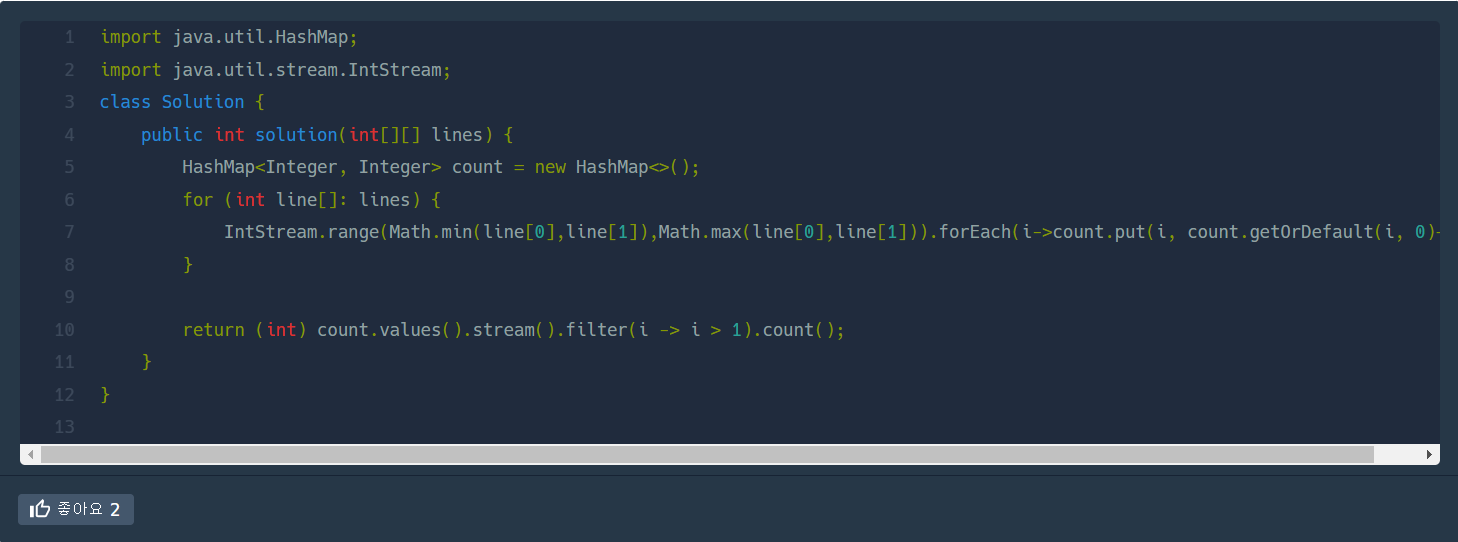
다른 풀이들은 거의 대부분 HashMap 클래스를 이용한 것 같다.
평행

대망의 정답률 29% 문제의 전 문제인데, 허무할 정도로 너무 쉬웠다. 이 문제도 수포자들의 관문이었던 모양이다.
특정 점들을 이은 두 직선의 평행 여부를 판단하는 문제인데, 평행 여부는 기울기를 통해 판단할 수 있다는 사실과 직선의 기울기를 구하는 방법만 알면 쉽게 풀 수 있다.
기울기는 x값이 특정 값만큼 변화할 때 y값이 얼마나 변화하는 지를 계산한 값이다. 따라서 (y2 - y1) / (x2 - x1)의 값을 구하면 된다. 이를 0에 가까운 극히 짧은 순간의 기울기를 구한 것이 미분이다.

삼항연산자를 이용해 선분의 기울기를 비교하는 세 가지 경우의 수를 계산했다.
그런데 테스트 하나를 통과하지 못했다. 아마 정수형으로 계산된 식이라 소수점 이하가 버려져 다른 결과값이 나온 것 같다.

실수형으로 고쳐 주니 나머지 테스트도 통과할 수 있었다.

다른 풀이들을 보니, 아마 내 풀이가 가장 짧은 것 같다. 좋아요를 가장 많이 받은 풀이는 2차원 배열을 이용했다. 뭔가 복잡하다.
'Coding Test' 카테고리의 다른 글
| Java 코딩테스트 연습 14일차 (프로그래머스 스쿨 Lv.0, 1186점) (0) | 2023.03.19 |
|---|---|
| Java 코딩테스트 연습 13일차 (프로그래머스 스쿨 Lv.0, 1183점) (0) | 2023.03.19 |
| Java 코딩테스트 연습 11일차 (프로그래머스 스쿨 Lv.0, 1146점) (0) | 2023.03.17 |
| Java 코딩테스트 연습 10일차 (프로그래머스 스쿨 Lv.0, 1130점) (0) | 2023.03.16 |
| Java 코딩테스트 연습 9일차 (프로그래머스 스쿨 Lv.0, 1100점) (0) | 2023.03.15 |



